jueves, 9 de junio de 2011

CAMPO VECTORIAL

En matemática un campo vectorial es una construcción del cálculo vectorial que asocia un vector a cada punto en el espacio euclídeo, de la forma 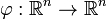\varphi:\R^n \to \R^n.

Los campos vectoriales se utilizan a menudo en la física para, por ejemplo, modelar la velocidad y la dirección de un líquido móvil a través del espacio, o la intensidad y la dirección de una cierta fuerza, tal como la fuerza electromagnética o la gravitatoria, pues cambian punto a punto.

En el tratamiento matemático riguroso, los campos vectoriales se definen en variedades diferenciables como secciones del fibrado tangente de la variedad. Este es el tipo de tratamiento necesario para modelizar el espacio-tiempo curvo de la teoría general de la relatividad por ejemplo.

Un campo vectorial sobre un subconjunto del espacio euclídeo X \subset \R^nes una funcióna valores vectoriales: \mathbf{F}: X \rightarrow \mathbb{R}^n \,

Decimos que \mathbf{F} es un campo vectorial Ck si como función es k veces diferenciable con continuidad en X.

Un campo vectorial se puede visualizar como un espacio X con un vector n- dimensional unido a cada punto en X.

OPERACIONES CON CAMPOS VECTORIALES

Dados dos campos vectoriales Ck F, G definidos sobre X y una función Ck a valores reales f definida sobre X, se definen las operaciones producto por escalar y adición:

(f \mathbf{F})(\mathbf{x}) = f(\mathbf{x}) \mathbf{F}(\mathbf{x})

Debido a la linealidad de la función (F+G):

\mathbf{(F+G)}(\mathbf{x}) = \mathbf{F}(\mathbf{x}) + \mathbf{G}(\mathbf{x})

define el módulo de los campos vectoriales Ck sobre el anillo de las funciones Ck. Alternativamente el conjunto de todos los campos vectoriales sobre un determinado subconjunto X es en sí mismo un espacio vectorial.

DERIVACIÓN Y POTENCIALES ESCALARES Y VECTORES

Los campos vectoriales se deben comparar a los campos escalares, que asocian un número o escalar a cada punto en el espacio (o a cada punto de alguna variedad).

Las derivadas de un campo vectorial, que dan por resultado un campo escalar u otro campo vectorial, se llaman divergencia y rotorres pectivamente. Recíprocamente:

  • Dado un campo vectorial cuyo rotacional se anula en un punto , existe un campo potencial escalar cuyo gradiente coincide con el campo escalar en un entorno de ese punto.
  • Dado un campo vectorial solenoidal cuya divergencia se anula en un punto, existe un campo vectorial llamado potencial vector cuyo rotacional coincide con el campo escalar en un entorno de ese punto.

Estas propiedades se explican se derivan del teorema de Poincaré.

PUNTOS ESTACIONARIOS

Un punto x en X se llama estacionario si:

\mathbf{F}(\mathbf{x}) = \mathbf{0}


El conjunto de todos los espacios vectoriales definidos sobre un subconjunto X, que son estacionarios en un determinado punto forman un subespacio vectorial del conjunto del espacio vectorial definido en la sección anterior

EJEMPLOS

  • Un campo vectorial para el movimiento del aire en la tierra asociará a cada punto en la superficie de la tierra un vector con la velocidad y la dirección del viento en ese punto. Esto se puede dibujar usando flechas para representar el viento; la longitud (magnitud) de la flecha será una indicación de la velocidad del viento. Un "Alta" en la función usual de la presión barométrica actuaría así como una fuente (flechas saliendo), y un "Baja" será un sumidero (flechas que entran), puesto que el aire tiende a moverse desde las áreas de alta presión a las áreas de presión baja.
  • Un campo de velocidad de un líquido móvil. En este caso, un vector de velocidad se asocia a cada punto en el líquido. En un túnel de viento, las líneas de campo se pueden revelar usando humo.

Campo gradiente

Los campos vectoriales se pueden construir a partir de campos escalares usando el operador diferencial vectorial gradiente que da lugar a la definición siguiente.

Un campo vectorial Ck F sobre X se llama un campo gradiente o campo conservativo si existe una función Ck+1 a valores reales f: X →R (un campo escalar) de modo que

\mathbf{F}(\mathbf{x}) = \nabla f(\mathbf{x}) \qquad (\mathbf{x} \in X)

La integral curvilínea sobre cualquier curva cerrada (e.g. γ(a) = γ(b)) en un campo gradiente es siempre cero.

\oint_\gamma \langle \mathbf{F}( \mathbf{x} ), d\mathbf{x} \rangle = \int_a^b \langle \nabla f( \mathbf{\gamma} (t)), \mathbf{\gamma}'(t) \rangle \, dt = \int_a^b \frac{d}{dt} f \circ \mathbf{\gamma}(t) \, dt = f(\mathbf{\gamma}(b)) - f(\mathbf{\gamma}(a)) = 0Campo central

Un campo vectorial C∞ sobre Rn \{0} se llama campo central si:

\mathbf{F}(\mathbf{O}(\mathbf{x})) = \mathbf{O}(\mathbf{F}(\mathbf{x})) \qquad (\mathbf{O} \in O(n, \mathbf{R}) \mbox{ , } \mathbf{x} \in R^n \setminus \lbrace 0 \rbrace )

Donde O(n, R) es el grupo ortogonal. Decimos que los campos centrales son invariantes bajo transformaciones ortogonales alrededor de un punto S. El punto S se llama el centro del campo.

Un campo central es siempre un campo gradiente, por los campos centrales pueden ser caracterizados más fácilmente mediante:

\mathbf{F}(\mathbf{x}) = -\left(\frac{\part U}{\part x}\mathbf{\hat{i}} + \frac{\part U}{\part y}\mathbf{\hat{j}} + \frac{\part U}{\part z}\mathbf{\hat{k}}\right)

Campo solenoidal

Otros campos vectoriales se pueden construir a partir de un campo vectorial usando el operador diferencial vectorial rotacional que da lugar a la definición siguiente.

Un campo vectorial Ck F sobre X se llama un campo solenoidal si existe una función vectorial Ck+1 A: X → Rn (un campo vectorial) de modo que:

\mathbf{F}(\mathbf{x}) = \nabla \times \mathbf{A}(\mathbf{x}) \qquad (\mathbf{x} \in X)

La integral de superificie o flujo cualquier superficie cerrada de un campo solenoidal es siempre cero.

\oint_{\partial V} \langle \mathbf{F}( \mathbf{x} ), d\mathbf{S} \rangle = \int_V \nabla \cdot (\nabla \times \mathbf{A})\ dV = \int_V 0\ dV = 0

Publicado por en

1 comentario:

Suscribirse a: Enviar comentarios (Atom)