Relación de recurrencia
Una ecuación recurrente es un tipo específico de relación de recurrencia, para la sucesión  es una ecuación que relaciona
es una ecuación que relaciona  con alguno de sus predecesores
con alguno de sus predecesores  .
.
Las condiciones iniciales para la sucesión 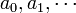 son valores dados en forma explícita para un número finito de términos de la sucesión.
son valores dados en forma explícita para un número finito de términos de la sucesión.
Resolver una relación de recurrencia consiste en determinar una fórmula explícita (cerrada) para el término general  , es decir una función no recursiva de n.
, es decir una función no recursiva de n.
Hay dos métodos para resolver relaciones recurrentes : iteración y un método especial que se aplica a las relaciones de recurrencia lineales homogéneas con coeficientes constantes.
Un ejemplo de una relación de recurrencia es el siguiente:
Algunas definiciones de recurrencia pueden tener relaciones muy complejas(caóticas) y sus comportamientos, a veces son estudiados por los físicos y matemáticos en un campo de las matemáticas conocido como análisis no lineal.
Recurrencia Lineales
Una relación de recurrencia es lineal de grado k si tiene la siguiente estructura:
siendo  funciones reales de
funciones reales de  , y
, y  una función de n.
una función de n.
El adjetivo lineal indica que cada término de la secuencia está definido como una función lineal de sus términos anteriores. El orden de una relación de recurrencia lineal es el número de términos anteriores exigidos por la definición.
En la relación  el orden es dos, porque debe haber al menos dos términos anteriores.
el orden es dos, porque debe haber al menos dos términos anteriores.
Ecuación de Recurrencia lineal homogénea con coeficientes constantes
Se llama ecuación de recurrencia lineal homogénea de grado k, con coeficientes constantes, a una expresión del tipo:
Para poder encontrar una solución, hacen falta unas condiciones de contorno o iniciales 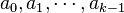 , siendo k el grado de la ecuación.
, siendo k el grado de la ecuación.
La recurrencia lineal, junto con las condiciones iniciales  , determinan la secuencia única.
, determinan la secuencia única.
Sea la ecuación de recurrencia lineal homogénea de orden k anterior, se denomina ecuación característica a la ecuación de grado k:
 g
g- La generación de la función racional
las secuencias lineales recursiva son precisamente las secuencias cuya función de generación es una función racional: el denominador es el polinomio auxiliar (a una transformación), y el numerador se obtiene con los valores iniciales.
El caso más sencillo son las secuencias periódicas,an = an − d, n≥d que tienen secuencia  y función de generación una suma de una serie geométrica:
y función de generación una suma de una serie geométrica:
Más general, dada la relación de recurrencia:
con función de generación
la serie es aniquilada por ad y anteriormente por el polinomio:
Eso es, multiplicando la función de generación por el polinomio
como el coeficiente en xn, que desaparece (por la relación de recurrencia) para n ≥ d. Así:
como dividiendo:
expresando la función de generación como una función racional. El denominador es xdp(1 / x), una transformación del polinomio auxiliar (equivalente, invirtiendo el orden de los coeficientes); también se puede usar cualquier múltiplo de esta, pero esta normalización es elegida por ambas porque la relación simple del polinomio auxiliar, y de ese modo b0 = a0.
Dada una secuencia  de números reales: la primera diferencia
de números reales: la primera diferencia 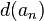 se define como
se define como 
La segunda diferencia  se define como
se define como  ,
,
que se puede simplificar a  .
.
Más general: la diferencia 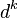 se define como
se define como 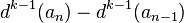
A diferencia de la ecuación es una ecuación compuesta por an y sus diferencias. Cada relación de recurrencia puede ser formulada como una ecuación de diferencia. Por el contrario, cada ecuación de diferencia puede ser formulada como una relación de recurrencia. Algunos autores así utilizan los dos términos intercambiables. Por ejemplo, la ecuación de la diferencia:
es equivalente a la relación de recurrencia:
De este modo se puede resolver relaciones de recurrencia por la reiteración como ecuaciones diferencia, y luego la solución de la ecuación de diferencia, análogamente como una solución de ecuaciones diferenciales ordinarias.
Ver escala de tiempo de cálculo para la unificación de la teoría de las ecuaciones de diferencia con la de las ecuaciones diferenciales.
Resolución
una ecuación de recurrencia lineal homogénea,  su ecuación característica y,
su ecuación característica y,  las raíces de la ecuación característica con multiplicidades
las raíces de la ecuación característica con multiplicidades 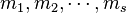 respectivamente. La solución de esta ecuación sería:
respectivamente. La solución de esta ecuación sería:
Con  el polinomio de grado menor o igual que
el polinomio de grado menor o igual que  . Para poder calcular los coeficientes de los polinomios
. Para poder calcular los coeficientes de los polinomios  , necesitamos saber las condiciones iniciales de la ecuación de recurrencia.
, necesitamos saber las condiciones iniciales de la ecuación de recurrencia.
Números de Fibonacci
Los números de Fibonacci están definidos usando la siguiente relación de recurrencia lineal:
con los valores iniciales:
La secuencia comienza: 1, 1, 2, 3 ,5, 8, 13, 21 ,34, 55, 89... El objetivo de la resolución de la ecuación de recurrencia es encontrar una forma cerrada para calcular los números de Fibonacci.
La ecuación característica es la siguiente:
por lo tanto, la solución general es:
Para hallar el valor de A1 y A2 resolvemos las siguientes ecuaciones:
Entonces:
y
La forma cerrada para los números de Fibonacci es:

- Ecuación de Recurrencia lineal no homogénea con coeficiente constantes
Recibe el nombre de ecuación de recurrencia lineal no homogénea de grado k, con coeficientes constantes, una expresión del tipo:  .
.
Resolución
La solución general sería:  , donde
, donde  es la solución de la ecuación de recurrencia lineal homogénea asociada es decir la ecuación :
es la solución de la ecuación de recurrencia lineal homogénea asociada es decir la ecuación :  y donde
y donde  es la solución particular que depende de la función F(n). Por lo tanto los pasos a seguir serían, primero calcular la solución de la ecuación homogénea, calcular una solución particular para F(n) y sumarla a la homogénea, y a continuación aplicar las condiciones iniciales para calcular las constantes. En la siguiente tabla, encontramos cuales son las posibles soluciones particulares:
es la solución particular que depende de la función F(n). Por lo tanto los pasos a seguir serían, primero calcular la solución de la ecuación homogénea, calcular una solución particular para F(n) y sumarla a la homogénea, y a continuación aplicar las condiciones iniciales para calcular las constantes. En la siguiente tabla, encontramos cuales son las posibles soluciones particulares:
| F(n) | 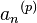 | ||
| C,constante | C0,constante | ||
| n | C0 + C1n | ||
| n2 | C0 + C1n + C2n2 | ||
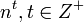 |  | ||
 | C0rn | ||
| ntrn | rn(C0 + C1n + C2n2) | ||
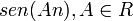 | C0sen(An) + C1cos(An) | ||
 | C0sen(An) + C1cos(An) | ||
 | C0rnsen(An) + C1rncos(An) | ||
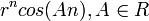 | C0rnsen(An) + C1rncos(An) |
Consideraciones:
1.- Si F(n) es una combinación lineal de algunas de las funciones de la tabla anterior, su solución particular es la combinación lineal de las soluciones particulares de esas mismas funciones.
2.- Si uno de los sumando de F(n) es el producto de una constante por una solución de la ecuación característica homogénea asociada, entonces es necesario multiplicar la solución particular correspondiente a este sumando por la menor potencia de n, n´ tal que este nuevo producto no sea solución de la ecuación característica homogénea asociada.
Ejemplo: Torres de Hanói
La ecuación de recurrencia asociada con el problema de las Torres de Hanói es la siguiente:
Con las condiciones iniciales:
Se resuelve la siguiente homogénea:
La ecuación característica es: x − 2 = 0, entonces x = 2
Entonces : 
A continuación, se resuelve la ecuación particular: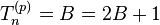 , entonces B = − 1.
, entonces B = − 1.
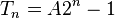 , entonces igualando con las condiciones iniciales la solución es :
, entonces igualando con las condiciones iniciales la solución es : 
Recurrencia No lineales
Para resolver recurrencias no lineales tenemos muchas opciones de las cuales:
- Buscar transformaciones o cambios de variables que hagan la recurrencia lineal.
- Para el caso
 , hay un teorema muy útil que es el Teorema Maestro.
, hay un teorema muy útil que es el Teorema Maestro.


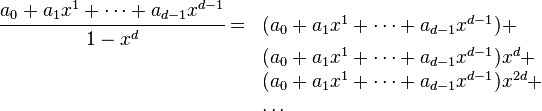
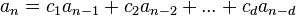

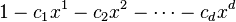
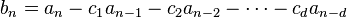
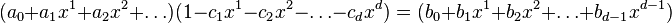

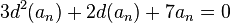
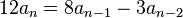

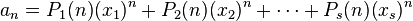
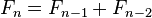

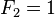
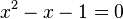
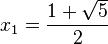
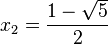

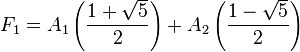
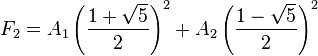

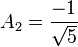


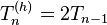
¡Te felicito! Tienes 10.
ResponderEliminar