Sucesión de Fibonacii
En matemática, la sucesión de Fibonacci es la siguiente sucesión infinita de números naturales:
La sucesión inicia con 0 y 1, y a partir de ahí cada elemento es la suma de los dos anteriores.
A cada elemento de esta sucesión se le llama número de Fibonacci. Esta sucesión fue descrita en Europa por Leonardo de Pisa, matemático italiano del siglo XIII también conocido como Fibonacci. Tiene numerosas aplicaciones en ciencias de la computación, matemáticas y teoría de juegos. También aparece en configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la disposición de las hojas en el tallo, en la flora de la alcachofa y en el arreglo de un cono.
Historia
Antes de que Fibonacci escribiera su trabajo, la sucesión de los números de Fibonacci había sido descubierta por matemáticos indios tales como Pingala (200 a.c.), Gopala (antes de1135) y Hemachandra (c. 1150), quienes habían investigado los patrones rítmicos que se formaban con sílabas o notas de uno o dos pulsos. El número de tales ritmos (teniendo juntos una cantidad n de pulsos) era fn + 1, que produce explícitamente los números 1, 2, 3, 5, 8, 13, 21, etc.1
La sucesión fue descrita por Fibonacci como la solución a un problema de la cría de conejos: "Cierto hombre tenía una pareja de conejos juntos en un lugar cerrado y uno desea saber cuántos son creados a partir de este par en un año cuando es su naturaleza parir otro par en un simple mes, y en el segundo mes los nacidos parir también".2
Dicho de otra forma, sirve para conocer el número de conejos (parejas de conejos) que habrá en 12 meses, si estos se reproducen continuamente y cada pareja de conejos produce una nueva pareja de conejos (un macho y una hembra). Cada conejo se puede cruzar a la edad de un mes, siendo su periodo de gestación un mes. Siendo así, se tiene que:
| Número de Mes | Explicación de la genealogía | Parejas de conejos totales |
|---|---|---|
| Fin del mes 0 | 0 conejos vivos. | 0 parejas en total. |
| Comienzo del mes 1 | Nace una pareja de conejos (pareja A). | 1 pareja en total. |
| Fin del mes 1 | La pareja A tiene un mes de edad. Se cruza la pareja A. | 1+0=1 pareja en total. |
| Fin del mes 2 | La pareja A da a luz a la pareja B. Se vuelve a cruzar la pareja A. | 1+1=2 parejas en total. |
| Fin del mes 3 | La pareja A da a luz a la pareja C. La pareja B cumple 1 mes. Se cruzan las parejas A y B. | 2+1=3 parejas en total. |
| Fin del mes 4 | Las parejas A y B dan a luz a D y E. La pareja C cumple 1 mes. Se cruzan las parejas A, B y C. | 3+2=5 parejas en total. |
| Fin del mes 5 | A, B y C dan a luz a F, G y H. D y E cumplen un mes. Se cruzan A, B, C, D y E. | 5+3=8 parejas en total. |
| Fin del mes 6 | A, B, C, D y E dan a luz a I, J, K, L y M. F, G y H cumplen un mes. Se cruzan A, B, C, D, E, F, G y H. | 8+5=13 parejas en total. |
| ... | ... | ... |
| Fin del mes 12 | ... | ... |
Nota: al contar la cantidad de letras distintas en cada mes, se puede saber la cantidad de parejas totales que hay hasta ese mes.
De esta manera Fibonacci presentó la sucesión en su libro Liber Abaci, publicado en 1202. Muchas propiedades de la sucesión de Fibonacci fueron descubiertas por Édouard Lucas, responsable de haberla denominado como se la conoce en la actualidad.3
También Kepler describió los números de Fibonacci, y el matemático escocés Robert Simson descubrió en 1753 que la relación entre dos números de Fibonacci sucesivos fn + 1 / fn se acerca a la relación áurea fi ( ) cuanto más se acerque a infinito; es más: el cociente de dos términos sucesivos de toda sucesión recurrente de orden dos tiende al mismo límite. Esta serie ha tenido popularidad en el siglo XX especialmente en el ámbito musical, en el que compositores con tanto renombre como Béla Bartók, Olivier Messiaen y Delia Derbyshire la han utilizado para la creación de acordes y de nuevas estructuras de frases musicales.
) cuanto más se acerque a infinito; es más: el cociente de dos términos sucesivos de toda sucesión recurrente de orden dos tiende al mismo límite. Esta serie ha tenido popularidad en el siglo XX especialmente en el ámbito musical, en el que compositores con tanto renombre como Béla Bartók, Olivier Messiaen y Delia Derbyshire la han utilizado para la creación de acordes y de nuevas estructuras de frases musicales.
Definicion formal
Los números de Fibonacci  quedan definidos por las ecuaciones
quedan definidos por las ecuaciones
(1)
(2)
(3)
para
Esto produce los números
y así sucesivamente de manera infinita.
Representaciones alternativas
Para analizar la sucesión de Fibonacci (y, en general, cualquier sucesión) es conveniente obtener otras maneras de representarla matemáticamente.
[editar]Función generadora
Una función generadora para una sucesión cualquiera 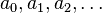 es la función
es la función 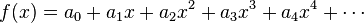 , es decir, una serie formal de potencias donde cada coeficiente es un elemento de la sucesión. Los números de Fibonacci tienen la función generadora
, es decir, una serie formal de potencias donde cada coeficiente es un elemento de la sucesión. Los números de Fibonacci tienen la función generadora
(4)
Cuando esta función se expande en potencias de  , los coeficientes resultan ser la sucesión de Fibonacci:
, los coeficientes resultan ser la sucesión de Fibonacci:
[editar]Fórmula explícita
La definición de la sucesión de Fibonacci es recurrente; es decir que se necesitan calcular varios términos anteriores para poder calcular un término específico. Se puede obtener una fórmula explícita de la sucesión de Fibonacci (que no requiere calcular términos anteriores) notando que las ecuaciones (), () y () definen la relación de recurrencia
con las condiciones iniciales
 y
y 
El polinomio característico de esta relación de recurrencia es t2 − t − 1 = 0, y sus raíces son
De esta manera, la fórmula explícita de la sucesión de Fibonacci tendrá la forma
Si se toman en cuenta las condiciones iniciales, entonces las constantes b y d satisfacen la ecuación anterior cuando n = 0 y n = 1, es decir que satisfacen el sistema de ecuaciones
Al resolver este sistema de ecuaciones se obtiene
Por lo tanto, cada número de la sucesión de Fibonacci puede ser expresado como
(5)
Para simplificar aún más es necesario considerar el número áureo
de manera que la ecuación () se reduce a
(6)
Esta fórmula se le atribuye a Édouard Lucas, y es fácilmente demostrable por inducción matemática. A pesar de que la sucesión de Fibonacci consta únicamente de números naturales, su fórmula explícita incluye al número irracional  . De hecho, la relación con este número es estrecha.
. De hecho, la relación con este número es estrecha.
[editar]Forma matricial
Otra manera de obtener la sucesión de Fibonacci es considerando el sistema lineal de ecuaciones
Este sistema se puede representar mediante su notación matricial como
Conociendo a f0 = 0 y f1 = 1, al aplicar la fórmula anterior n veces se obtiene
(7)
Una vez aquí, simplemente tenemos que diagonalizar la matriz, facilitando así la operación de potenciación, y obteniendo por tanto la fórmula explícita para la sucesión que se especificó arriba.
y más aún
(8)
Estas igualdades pueden probarse mediante inducción matemática.

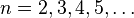




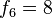

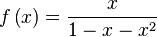
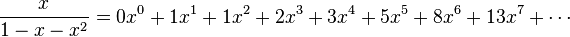
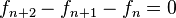
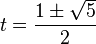


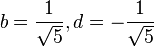
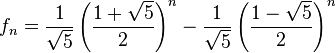
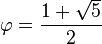
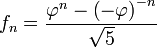
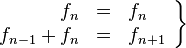
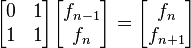

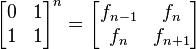
Chely,
ResponderEliminarmuy buen trabajo.